2.1 Scalar Effective Length

We begin with the simplest possible example, and study a thin-wire receiving dipole of length 2h, placed along the  axis, with a gap at its center. A linearly polarized plane wave is incident, as shown in Figure 2a, where for the moment we assume that the direction of polarization is such that the electric field is in the plane determined by the antenna and the direction of propagation of the wave. The incident electric field, is in the same vector direction as that of the electric field that would have been produced if we had been transmitting with this antenna: i.e., transmitting with an upward-directed phasor current, , entering the upper half of the dipole at the center, which means that far zone electric field radiation is in the direction of the unit vector . Let us assume that this incident field arises from a specific source-a distant loop antenna-shown in Figure 2a. The centers of the loop and the dipole are separated by a distance , The field of an electrically small circular loop antenna is derived in most courses in antenna theory (e.g., [2, Section 7.5]). If the loop is of radius  and if it carries a current  circulating in the counterclockwise direction as shown, the electric field in the counterclockwise direction as shown, the electric field in the loop's plane at  meters from the loop's center is

where  and 

Here, the direction of the field is in the same sense a s the current flow. We want this to be identical to the given field striking the antenna. Hence,

which we solve to obtain

This is the current on the loop that will create the given electric field striking the center of the dipole.

Now, we remove the current generator supplying the loop antenna with current, and leave behind a small gap. As shown in Figure 2b, we fill the center of the dipole with a current generator supplying the currentfound in Equation (3). We next apply the theory of reciprocity, familiar to most students from their courses in circuit theory.If they need convincing that the formula applies to circuits that are coupled by electromagnetic radiation, they may refer to [5]. The voltage in the gap of the loop, , must be identical to that which had appeared in the gap of the dipole when the loop was supplied with current . This voltage is easily found using Faraday's law of induction. For the moment, we assume that the dipole is electrically very thin, and thatwhere  is any integer. Most textbooks on antennas or electromagnetic theory assume that the upward current, , along the thin center-driven dipole (if it is less than one or two wavelengths in size) is then well approximated by

Students learn (see, e.g., [6]) that the far-zone fields created by a center-driven dipole with this current distribution are given by

and

where . Here,

The loop is assumed to be small enough so that the magnetic field striking its center is identical to the magnetic field striking anywhere in its enclosed area. The magnetic field caused by whatever current appears on the open-circuited loop due to incident fields is assumed negligible. In Figure 2b, the magnetic flux, , threading downward through the plane of this page when the dipole is driven with current  is thus the product of the magnetic-flux density in Equation (6) with the area of the loop:

By Faraday's law of induction (i.e., here, , this implies that the voltage in the gap is

Using  from Equation (3) in the preceding, we have

where we have used .

We know by reciprocity that  in Equation (10) is the voltage induced in the gap in the dipole in Figure 2a.

We now make this definition:

If a receiving antenna is exposed to a linearly polarized electric field associated with a plane wave coming from a particular direction, and if this field has the identical (linear) polarization to that which would occur if the antenna were transmitting in that direction, then the product of the (scalar) effective length of the antenna, , for that direction and the incident phasor electric field will yield the voltage induced in a small gap in this antenna. The incident field is defined at the gap.

The preceding tacitly assumes that we are dealing with an antenna that when transmitting produces a linearly polarized wave in its far zone. There is also an implicit sign convention: If the voltage appearing in the gap when we are receiving is designated, then the electric field created when transmit is such that the current enters terminal 1.

With this definition, we see that the effective length of the dipole studied here is the ratio of voltage to field from Equation (10):

Notice how the transmitting pattern of the dipole, , estab-lishes the receiving property . The preceding can yield some results that might look familiar. If we are employing a half-wave dipole, where , then Equations (7) and (11) yield

from which, if , Equation (12) tells us that the effective length is  times the actual antenna's length.

If when driven at the center the dipole is electrically short, so that , the distribution of current along its length is approximately triangular. Using small-argument expansions  ‘ and  in Equations (7) and (11), we have for a short antenna,

The effective length of an electrically short receiving antenna is thus at best , half the actual length 2h, and this occurs when.

2.2 Vector Effective Length

Suppose the antenna in Figure 2a had been exposed to a plane wave the electric field of which possessed a component , as shown in Figure 3a. This component is normal to both the direction of the electric field produced in the far zone by the antenna when transmitting, and to the direction of propagation of that wave. We can use reciprocity and the loop antenna to argue that this new component, , will have no effect on the open-circuit voltage appearing in the gap. We simply imagine this component to have been produced by a current-carrying loop antenna with a normal in the direction  as shown in Figure 3 a.

Now, this same current, when supplied to the dipole, will produce a far-zone magnetic field lying only in the direction . No magnetic flux lines pass through the plane of the loop (see Figure 3b), and Faraday's law indicates there is no voltage induced in the loop. By reciprocity, no voltage will thus appear in the gap of the dipole when exposed to the electric field shown in Figure 3a. The dipole responds only to the component of electric field in the direction of  The preceding can be generalized:

A receiving antenna, with an open circuit (a gap) for its load, exposed to an incoming plane electromagnetic wave of arbitrary linear polarization, will produce a voltage in the gap in response to only that portion of the wave the electric field of which is along the direction of the electric field created by the antenna if it were transmitting in the direction from which the incoming radiation is incident.

Since it speaks of the direction of the electric field, the above assumes that the antenna creates a linearly polarized wave when transmitting into its far zone.

From the above statement, it becomes natural to define a vector effective length for a receiving antenna: The vector effective length of a receiving antenna, , exposed to a plane wave arriving from direction , is the product , where  is the (scalar) effective length for reception from that direction, and  is the unit vector in the direction of the electric field created in the direction , if we use the receiving antenna for transmit-ting. The voltage induced in the gap of the antenna by an incident electric field is thus given by

The use of the vector effective length and Equation (14) thus ensure that the voltage induced in the gap of a receiving antenna is a response only to that portion of the incident electric field having the polarization that causes the voltage to appear.

2.3 Further Generalizations and More-Complicated Antennas

The electric field in the far zone of an antenna radiating into free space can be cast into the form

where  is the current supplied by the generator feeding the antenna. We assume this generator to be located at the origin. Justification for this equation can be found in [6, Section 12.4], and would be taught in most courses in antenna theory under the rubric ‘'far-field approximation.” We have modified the traditional expression by including a factor  for the phasor current supplied by a (single) source of energy. With an application of to the above, and retention of only the far-zone terms, we have that the magnetic flux density Is

Figure 3a. The incident electric field is normal to the wire dipole.

Figure 3b. The magnetic flux density vector is parallel to the plane of the loop.

If this antenna is used for receiving, with incident fields at the origin having components  and , we can obtain the voltage produced in the gap by following the method of reciprocity, as used above. We will require the use of two small loops to produce the two components of field. If only  is incident, then we assume it to have been produced by a loop antenna such as that shown in Figure 2a, where the current is given in Equation (3), and we take  as . Applying this same current to the dipole, determining the voltage, , by means of Faraday's law, and noting that only the portion of the magnetic flux density  is required for our calculation, we proceed as above and find .

If just  was incident, we would assume it to have been created by a loop antenna such as that shown in Figure 4a. The current circulating in the direction of the arrow on the loop would have to be

Note the minus sign. If we apply this current to the antenna and compute the voltage induced in the loop of Figure 4b by means of Faraday's law and the vector component of the magnetic flux density  ‘, we find that the voltage, , is . With electric field , incident on the receiving antenna and striking a gap in the antenna at the origin of the coordinate system, we thus have a voltage across the gap

From this we can make the following generalization: If the far-zone electric field of an antenna in free space, with generator at the origin supplying current , is stated in the form

Figure 4a. The component  is created by a loop with the plane normal to

Figure 4b. The loop in Figure 4a is used for reception.

The voltage induced in the gap of the antenna by an incident linearly polarized plane wave is given by Equation (14).

The assumption of linear polarization means that  and  are in phase or out of phase. We can immediately put the preceding to work. It is a standard exercise (see [3, p. 159]) to show that an electrically short antenna, also known as the elementary or Hertzian dipole, of length 2h (or ), centered at the origin and having a uniform upwardly directed current, , along the z axis, creates an electric field. From this, we see that the vector effective length isThis is a well-known result.

One can of course apply Equations (18) and (19) to antennas that are not necessarily confined to the  axis. A good exercise is to derive the vector effective length for the electrically short 90° Vantenna shown in Figure 5. Here, we assume that that the two legs of the antenna are so short that the current distribution on them, when transmitting, is given by  and  on the wires, except in the small gap containing the current generator. The resultant vector effective length is

The preceding indicates that if a plane wave were incident on the antenna, and polarized only in the direction of , then the resultant voltage in the gap will be maximum if we choose  and  radians, which is intuitively satisfying.

Another possible exercise is to show that for a wire dipole antenna aligned along the axis, driven with current , and having a current  along its length, the far-zone electric field can be given by

where

and the integral is taken along the portion of the  axis carrying the wire. The effective length is given by , which simplifies to

2.4 Antenna Driving a Load

An antenna usually doesn't have an open circuit as its load. Most students are willing to accept that Thevenin's theo-rem, learned in their courses in circuit theory, will still be valid when the coupling between the input and output of a system is by means of electromagnetic waves. Ifwe thus place a complex impedance in the gap of any of the antennas dealt with so far, the voltage across this load can be computed, if we use the Thevenin equivalent circuit shown in Figure 6. Here, the Thevenin driving voltage is simply the voltage appearing in the gap if the load were replaced by an open circuit. Thus, . The Thevenin impedance is that impedance seen looking into the antenna when all sources of energy in the universe have been removed. For a loss less antenna in free space, this impedance would be of the form whereis the radiation resistance of the antenna, while  is the effective series reactance seen looking into the antenna. More generally, , where  takes into account ohmic losses occurring when the antenna is used for transmitting. Let a conjugate matched load be applied between terminals 1 and 2 of the receiving antenna, so that. This load now appears between terminals 1 and 2 of the circuit in Figure 6. We obtain the maximum available power at the load, which is

Figure 5. A V antenna.

Figure 6. The Thevenin equivalent circuit for the receiving antenna.

If the incident electric field, which is linearly polarized, is oriented along the vector effective length, , the preceding expression is maximized and simplifies to

where the magnitude signs refer to the magnitude of complex scalar phasors.

For a linearly polarized plane wave, the time-averaged flux of power in watts per square meters is . With this used in Equation (21), we obtain

where 

is known as the maximum effective area of a receiving antenna. Its use assumes that the incident radiation is polarized so as to maximize the power to the load, and it relates the incident time-averaged Poynting vector to the power delivered to an ideal load. The electric field in this instance must be along .

It is commonly assumed that the radiation resistance of a thin half-wave dipole is about 73.2 ohms. Neglecting any ohmic losses in the antenna, so that , and using Equations (12) and (23), we obtain the effective area of a half-wave dipole of length 2h as

The preceding discussion should be sufficient for a first classroom lecture on effective length in an elementary course. However, some instructors may wish to consider how to use the concept of effective length when the receiving antenna is a base-loaded monopole placed over an infinite perfectly conducting ground plane. This matter is treated here in the Appendix.

COMMENTARY

To see the advantages of the argument just presented, let us see how three standard texts treat the receiving antenna. Reference [1, p. 397] said, “The interaction of the incident electric field  with the receiving antenna is facilitated by the concept ofvector effective length of an antenna, , which is defined through [where]  is the open circuit voltage across the antenna terminals…. The receiving antenna relation applies to any antenna and is very intuitive.” The need for taking the conjugate of  in the preceding was never explained, and indeed the conjugate does not appear in handbook formulas on this subj ect, e. g., [4]. Reference [1] gave as anexample the computation of the vector effective length of an “ideal dipole,” an electrically short center-fed antenna containing a uniform current, , The authors observed that the electric field of this device when used in transmitting was , where  is the antenna length and  is the free-space wavenumber. They continued by saying that “since  contains information on the size of the antenna and the angular dependence of the radiation pattern we can write  where  “

The preceding is certainly not a proof that the last equation is the vector effective length of an ideal dipole. Indeed, had the writers used , which is certainly valid, they might have argued that  · The example gave no clue as to how to obtain the effective length of an antenna of a different length, or one with a nonuniform current distribution.

This matter is treated further, on page 472, where effective length is redefined by a new equation,  “where  is the antenna effective length upon receiving.” We are warned that this differs from the previous definition, and told that the present one can be found in a doctoral dissertation, perhaps leading the reader to think that its derivation is difficult.

Moving to reference [2], we find that vector effective length (here called “[vector] effective height” ) is treated asa footnote on page 31, while the main material on pages 30 and 31 describes a scalar “effective height,” . The defining equation is , which does not warn the reader that the voltage induced in the gap of the receiving antenna is a function of both the direction from which the incoming radiation is incident as well as the polarization of that radiation, although there is a remark about the antenna being “oriented for maximum response.” Having introduced this definition, the book asserts that because a half-wave dipole exhibits a sinusoidal current, its effective length is  multiplied by its actual length. The logic of this statement is unclear. The matter of polarization mismatch is treated in the footnote.

On page 31, the book observes that ) now redefined as , can be obtained from , the current along the antenna when used for transmitting. The equation given is

where  is the actual physical length and  is the current now supplied in the gap by a generator. As can be seen from the derivation of Equation (20), the above equation is mis-leading, as it is valid only for one particular angle of incidence of the received wave. The same text also observes that “effective height is a useful parameter for transmitting tower type antennas,” but the use of such antennas assumes a conducting Earth and there is no indication of how the preceding formula accounts for its presence.

Looking at the third text, [3, p. 88], we find that the vector effective length  “is a far field quantity and is related to the far zone-field  radiated by the antenna, with current  in its terminals by…

The author maintains that the open-circuit voltage of a receiving antenna is given by , where  is the incident electric field. No attempt is made to prove that the  appearing in his first equation (which describes transmitting) can be used in the second (which describes receiving)-although he lists six references to literature that presumably give the connection. Incidentally, had the author chosen to write  , his definition would have been in conformance with the one given here (see Equation (18)), as well as with common usage.

CONCLUSION

The preceding material is suitable for an introductory course in antennas. Because the radiated field of an electrically small loop antenna is essential to the discussion, it will perhaps be necessary to derive this field earlier in the course than is ordinarily done, in order to apply the method given here. As the field of a small loop is invariably taught in an introductory course in antennas, this juggling in the order of topics should create no hardship. The exposition of effective length presented leads seamlessly to the subject of effective area, and serves as a warning that one must be concerned with the possibility of polarization mismatch in applying .

method that we have introduced implicitly requires that the antenna the effective length of which we are seeking is one for which the transmitting pattern is known. This, in tum, requires that we know the current on the antenna when it is transmitting. In the case of wire or thin tubular antennas, especially dipoles, a considerable literature exists on this subject, e.g. [8].

In a more-advanced course, students can be encouraged to extend the subject of receiving antennas to more complicated situations in which the antenna is receiving an elliptically polarized wave, and/or when the antenna itself is capable of generating such a wave when transmitting. The problem of a receiving wire antenna parallel to a reflecting surface might also be studied.

APPENDIX: USE OF A GROUND PLANE

A receiving antenna often consists of a vertical wire placed at right angles to a perfectly conducting ground plane, with a load placed between the bottom of the antenna and the plane. Suppose a plane wave is incident on this monopole arrangement, as shown in Fjgure 7a. We will assume that the electric field is polarized only along , as any field component along  would have no effect at the load. Proceeding as before, we will assume that this electric field is created by a loop antenna above the ground plane. The current on the loop antenna is given by Equation (3), and the incident field striking the monopole at its base is . This is not the total field experienced by the monopole at , as it fails to account for the electric field of the wave reflected off the ground plane. The total field at  is, of course, normal to the plane.

Figure 7a. A receiving monopole above an infinite ground.

Figure 7b. The monopole and loop of Figure 7a and their images.

To compute the voltage appearing at the gap between the bottom surface of the monopole and the ground plane, we apply the method of images. This means we eliminate the ground plane, and introduce the image of the monopole and that of the loop antenna just described. The result is shown in Figure 7b. The monopole plus its new image now comprise a dipole, and the voltage across the gap in this dipole is the sum of the voltages created by the original loop and its image. the voltage created across the gap by the upper loop is simply , where  is the effective length of a dipole the upper half of which is the given monopole. By symmetry, the lower loop creates an identical voltage in the gap. The total voltage in the gap of the dipole is thus . We return to Figure 7 a and see that from a symmetry argument, the voltage existing at the base of  the monopole with respect to the ground plane is one-half the preceding result. The incident field, , creates an open-circuit voltage , or , where  is the vector effective length of the corresponding dipole in the absence of the ground plane. To summarize:

The vector effective length of a base-driven monopole antenna that is perpendicular to a perfectly conducting infinite ground plane is identical to the vector effective length of a dipole (in the absence of the ground plane) the upper half of which is that monopole.

To take a simple example, we have shown above that a half -wave conventional dipole antenna has a vector effective length , which means that a quarter-wave monopole, loaded at its base, has the identical vector effective length.

The voltage, , appearing in the gap between the lowest point on the monopole and the ground plane is

where one must keep in mind that  is the incident field at the base, not the total field. The total field is in fact perpendicular to the ground plane, and has the value  at the base, as can be seen if we analyze the reflection of a plane wave from an infinite ground plane.

The effective area of a loss less antenna in a lossless environment is found from Equation (23) to be  ‘ since . Now a lossless monopole antenna driven above an infinite ideal ground plane has an effective length equal to that of the corresponding dipole, as noted above. However, it is well known that the radiation resistance, , of this monopole is one-half that of the corresponding dipole in the absence of the plane, since radiation takes place from the monopole only in the half space above the ground plane. We see from the preceding formula for that the effective area of a monopole antenna driven over an ideal ground plane is twice that of the corresponding dipole in the absence of the ground plane. Since antenna gain is proportional to effective area, a monopole above an ideal ground plane has twice the gain of the corresponding dipole in the absence of the plane.

Acknowledgment

The author would like to thank an anonymous reviewer as well as Dr. Robert J. Mailloux for comments that have vastly improved this paper.

Culture, Technology, Britannia: The BBC Handbooks 2011 A. David Wunsch

Abstract

The BBC Handbook was a remarkable annual publication of the British Broadcasting Corporation during its formative early decades-- its “golden age.” The Handbook is of interest to collectors of books germane to radio history, to students of British broadcasting, to researchers of radio’s technical past and to historians of the UK of the 20’s, the depression, the war and postwar years. Handsomely designed, the volumes provide a description of how the BBC wished to present itself to the public and are remarkable not only for the technical sophistication assumed in its readers but for their record of the rich world of music, literature and theatre to which British wireless listeners were exposed. The Handbooks reflect the philosophy of the BBC founding director, Sir John Reith, a disciple of Mathew Arnold and his conception of culture.

HANDBOOK & YEARBOOK

In the 1920’s the new medium of radio broadcasting had a surprisingly beneficial effect on the much older medium of print. Many readers of this journal doubtless collect magazines for radio hobbyists that were generated by the “radio craze” of that decade. If you are shopping in a secondhand bookshop, perhaps looking for old copies of Gernsbach’s Radio News, see if the store has back issues of a publication that appeared annually, The BBC Handbook. The Handbook was a substantial publication—initially hardbound-- sometimes running over 450 pages which began in 1928 and last appeared in 1973.1 The BBC inexplicably elected to change the name of their book to either The Yearbook or The Annual on various occasions although the content and style of the publications remained mostly unchanged.2 Bibliophiles will want to give their attention to books of the period 1928-1946 and try to obtain copies with dust jackets. The BBC commissioned serious artists for these designs who often favored the then fashionable Art-Deco style. Figure 1 shows the cover for the 1929 issue.3 By the 1950’s the covers were-- to put it baldly—dull. What can be discovered from reading these books? You can learn the story of the British Broadcasting Corporation as it wished to present itself to the world. Such history has limitations and the serious student of the BBC will scale the highly readable Mount Everest of the subject: Asa Briggs’s 5 volume History of Broadcasting in the United Kingdom, while someone of more modest ambition might try Andrew Crisell’s An Introductory History of British Broadcasting whose 2nd edition was published in 2002.

COMPANY & CORPORATION

The letters BBC once stood for the British Broadcasting Company, the forbear of the present Corporation. The Company, a monopoly created by statute of the British government, was the only entity permitted in the UK to broadcast to the public, and was owned by British companies manufacturing receiving sets, e.g., Marconi, and Metropolitan-Vickers. These members were required to pay to the BBC a 10 percent royalty on radios they sold. An additional source of revenue would be an annual 

10 shilling licensing fee required of all households with radio sets—this money to be collected by the British Post Office which initially gave half of it to the Company.5 Licenses were to be granted to those set owners whose receivers were made by the member companies—which meant British companies. 6 The first Company broadcasts began on November 14, 1922 from London. From its very start, advertising on the new BBC was forbidden and the number and placement of new transmitting sites carefully regulated--a decision based in no small part on how negatively the founders viewed American broadcasting in the twenties.7 By 1925, about 80% of the population of the British Isles could receive the BBC.8 The directors of the new Company appointed as its fi rst General Manager John C. W. Reith, (1889-1971), whose name we will encounter throughout this essay.

The British Broadcasting Company was a profit-making institution. Public, nonprofit broadcasting in the UK began on January 1, 1927 when the British Broadcasting Corporation went on the air, replacing the Company. Although the reasons for this regime change are complex, much of the impetus came from Reith, who had a vision of the BBC as a vast educational and cultural public service—one that would be compromised by its connection to a profit-making company. Adding to the pressure for change was Reith’s resentment of the power held by the Post Office to restrict broadcasting of politically controversial material.  

The Crawford Committee, created by the Government to steer the future of broadcasting in Britain, issued its report in 1926, and the result was the formation of the Corporation—a nonprofit institution to be financed by license fees and enjoying a monopoly in radio. Because the new Corporation was authorized by a Royal Charter (which would periodically have to be renewed by the Government) and not by Parliamentary statute, it would have the appearance of being immune to political pressure. The Director-General of the Corporation was John Reith, (who was now Sir John); he held this title until June of 1938 when he resigned. 10 Some refer to his stewardship as The Golden Age of Wireless, and indeed this is the title of volume 2 of Briggs’s vast history.

Each Handbook/Yearbook was devoted in considerable part to a discussion of the content of the previous year’s programs.11 Just a cursory glance shows that this material might, in today’s discourse, be described with the pejorative “elitist.” Even now, mention of the Reith era BBC can stir up passions deriving from class resentment. To understand this BBC culture one must know something of the man at the top. 

My colleague at the University of Massachusetts Lowell, Todd Avery, has written a fi ne account of the Reithian BBC years, Radio, Modernism: Literature, Ethics, and the BBC 1922-1938. Some of the book deals with the profound influence that the writing of the English poet and essayist, Matthew Arnold (1822-1888), had on the BBC head. Readers may be familiar with his poem “Dover Beach” but more germane to our discussion is Arnold’s much quoted 1869 essay Culture and Anarchy – a defense of what is now called highbrow culture. Arnold recommends “culture as the great help out of our present difficulties; culture being a pursuit of our total perfection by means of getting to know, on all the matters which most concern us, the best that has been thought and said in the world….” [italics added]. Avery sees this as Reith’s “cultural agenda” for the BBC. For Arnold (and doubtless for Reith) anarchy was “doing as one likes.”

Arnold and Reith part ways in the matter of religion. Raised in a liberal Protestant household, Arnold was to become an agnostic—a fact evident in Dover Beach where the balm proposed for the loneliness and misery of man in an indifferent Godless world is: “Ah, love, let us be true/ To one another… .” Reith, the son of a minister of Church of Scotland, practiced a strict Calvinism, and could be hard on his employees, e.g., firing the BBC’s Chief Engineer after his being named as a co-respondent in a divorce proceeding.

THE NEW BOOKS

The first two Handbooks, dated 1928 and 1929, deserve some scrutiny as they set the tone for these publications up to the outbreak of the Second World War. The BBC broadcast no commercials but there was no such ban in their print publications. Looking through the advertising in these early books one sees how rapidly technological change was affecting radio design. Although the crystal  set was nearly obsolete, page 370 of the 1929 book carries an advertisement (Figure 2) for an improved crystal detector, the Excel, which brags of requiring no cat’s whisker. In advertisements for complete receivers we find quite a choice: crystal sets, and receivers of two or three valves (as the British called tubes) powered by batteries or the power mains. For accessories, we find ads for headphones as well as loudspeakers including the relatively new moving coil speaker, and a cornucopia of ads for batteries and battery eliminators as well as individual components (for the home set builder) e.g., coils, condensers, tube sockets, valves. For this reader what is striking about the advertisements for receivers is the number of sets being promoted that had only two or three valves at a time when American magazines promoted a plethora of radios with 5 or more tubes. Figure 3 shows an advertisement from page 389 of the 1930 Yearbook for a 2 valve radio. This American-British disparity doubtless arose from the crowded air waves in the US which

Figure 2. Crystal detector advertisement, 1929 Handbook

would have demanded receivers having high selectivity in contrast to the UK where typically one could hear only one to three BBC stations; to be sure, British listeners often received broadcasts emanating from the European continent. In the 1931 Yearbook (page 131) there is an article “The American Listener – A British Impression” in which the visitor from the UK is struck that “two out of every three receiving sets are five or six valve sets… The American Listener expects to be able to tune in easily to a dozen or more stations…”

The introduction to the first Handbook was written by Reith himself and he states his manifesto: the BBC is to be “of public service.” He is motivated by “the state of things in America,” i.e., the world of radio commercials and, even worse, interference among radio stations, not to mention program material that he regarded as vulgar and unworthy of broadcast.

Part of public service in Reith’s view is the purely technical: setting up transmitters such that the whole British population would be in “crystal range.” He extols a “common sense” censorship and as to news broadcasting, it must be “accurate brief and impartial.” For music, “good music is preferred to bad” and he intends to broadcast “music that is addressed to the finer and quieter sources of emotion in a small audience” but he does not shrink from his intention to broadcast “challenging new work.” As for religious content, he’s equally straightforward: the BBC has and will continue to broadcast “a nonsectarian Christianity –confined in respect of doctrine, to those simple essentials to which all Christians of the west can adhere.”

The 1928 book notes that “ The BBC observes Sunday in a religious non-sectarian way. Religious services are broadcast regularly from all stations, and no entertainment alternative is recognised.” Reith’s Calvinism is evident--you cannot avoid hearing a religious broadcast by switching to another BBC station. For nonbelievers, the temptation to listen to a secular broadcast in English from France or, later, Luxemburg was strong.

The BBC Handbook of 1928 was 384 pages in length while for 1929 –a depression year—it was 100 pages longer. One purpose of each volume was to give a summary of the previous year’s activities of the Corporation. Since advertising made up 5-10 percent of the pages of the book, one might wonder what filled these hundreds of pages, and here it becomes evident how broadly conceived these volumes were.

First, the books contain much material on the rapidly advancing technical achievements of the BBC—improvements to broadcasting from the London site as well as regional broadcasting from such places as Wales, Scotland, & Northern Ireland. Listeners in the London area are told in the 1929 book that soon they will be able to hear two different BBC stations (one national and the other regional) and are warned that they will need receivers of sufficient selectivity to separate the two signals, which will be broadcast from identical locations in North London but on different wavelengths. We’re informed of progress in Empire Broadcasting, meaning short wave service directed at the colonies and commonwealth countries.

Americans might be surprised to learn that, while much of BBC broadcasting in its first few decades took place within a spectrum of medium wave frequencies (comparable to the U.S. AM band), in 1925 the BBC opened a popular long wave station, 5XX, at 200khz (1,500 meters) radiating 25,000 watts. The station was situated in Daventry, near the center of England, and a picture of its antenna can be found on page 56 of the 1928 Handbook. Because of the long wavelength, the antenna had to be enormous and was supported by masts 500 feet high set 800 feet apart.14 The low frequency was chosen because of the resulting low attenuation of the ground wave; in this respect they were following in the footsteps of Marconi and his early wireless telegraphy work. Page 39 of the same book asserts that this step allowed 80 percent of the British population to receive the BBC without interruption via a mere crystal set. It was the fi rst long wavelength station in the world to give regular programming.

On page 92 of the 1928 Handbook we are reminded of the bete noir of the BBC: the unlicensed receiver. Readers are advised: “It is illegal to operate a receiving set without first taking out a licensing costing 10 s [shillings] a year, from the Post Offi ce. Some people do manage to listen without a license, but it costs much more in the end. It costs a lot more in self respect.” Note the allusion to one’s honor. This was already an old problem. A Profi le of the BBC written for the 1973 Handbook remarksthat when an amnesty was offered in 1923 to “license dodgers,” the number of licenses issued doubled in 10 days. How much was 10 shillings worth ? It wasn’t trivial. The average weekly pay of a coal miner in Britain in 1927 was 53 shillings for a 5.5 day work week. 15 A radio license could represent a day’s pay for a manual worker. The temptation to assemble a set from parts and not license it must have been enormous, particularly since there was no shortage of hobbyist magazines with instructions on this very subject.16 Incidentally, the Yearbook/Handbook cost from 2 to 2.5 shillings from the 1920’s through most of the 1940’s.

THE THIRTIES

Much of each annual describes the content of the previous year’s programs, and we suspect that were Mathew Arnold present to hear the wireless, in the Reith era, he would have been pleased. In the Panorama of Music for the 1930 Yearbook we learn that it is BBC policy to present as many works as possible by such composers as Haydn, Schubert, Bach, Handel and Mozart, and that these are the “bread and butter” of the daily fare of the lover of music. The BBC’s panorama consisted of live concerts of chamber, symphonic and operatic works not to mention—in 1929—a regular weekly series of Bach Cantatas as well as 13 weeks of music devoted to Schubert’s Centenary. Although all the composers were white and male, not all were dead; Stravinsky and Delius, still in the land of the living, had their work conducted by Sir Thomas Beecham. The 1930 book contains a touching photograph of the aging Delius, then blind and living in France, while the previous year’s volume has a full page photo of Arnold Schoenberg (the father of twelve tone serial music) and his fur clad wife. This often difficult composer had come from Germany to rehearse and conduct the British National Orchestra in his work “Gurrelieder .”

The BBC’s commitment to serious music is even more evident in the 1931 Yearbook, which reports the founding of the legendary BBC Symphony Orchestra the previous year. Starting in 1930 the new orchestra was conducted by Adrian Boult and consisted of 114 full-time players tied to a “no deputy” system- which meant that if you were a member of this august body you’d better show up for work and not appoint someone to take your place because you had another gig.17 Pages 176-77 of the book shows a two page photo spread of the orchestra together with the name of every player. What is striking is the large (for its day) number of women in the ensemble. Of the 14 first violinists, 8 are identifiable as female. Where did the money come from to pay for what was to become one of the world’s great symphonies? The answer is on page 39 : BBC license fees and revenues from publications adding up to over 1 million pounds for the year ending in 1929. One might contrast this orchestra with its closest American counterpart: the NBC Symphony, which, although it could boast of a very great conductor, Arturo Toscanini, wasn’t founded until 1937 and was to last only 17 years. The BBC Symphony today is still one of the world’s outstanding orchestras.

Reading through all of these Handbooks/ Yearbooks one should notice not only what is present but what is missing. The BBC took some risk in broadcasting the works of modern composers like Stravinsky, Bartok and Schoenberg. However, searching through these books of the twenties and thirties, one fi nds almost nothing about jazz. Reith is alleged to have hated the idiom.18 Instead, we fi nd plenty of dance band music. Indeed, the BBC formed its own dance orchestra ahead of the BBC Symphony, a fact gleaned from pages 200-201 of the 1929 Handbook. Having listened to recordings of British dance orchestras of this period I can say that these were housebroken versions of American jazz, divorced from the black influence, ethnicity, and daring that you might fi nd in some of the great U.S. jazz groups of the era led by, e.g., Fletcher Henderson, Benny Goodman, and Count Basie.  It would be wrong to accuse the BBC of racial prejudice: The 1930 Yearbook lists a July 1928 concert by the famed American Negro contralto Marian Anderson who carried an aura of high culture and could stun audiences with arias from great operas as well as the spirituals of her race. The 1931 Yearbook features a prominent photograph on page 114 of the great American Negro singer and actor Paul Robeson, who sang on the BBC.

Robeson appears on a list of Musicians of the Year. To look through these names is to be filled with envy for what listeners could have heard: under conductors we find Sir Thomas Beecham, Malcolm Sargent, Bruno Walter, Toscanini, and Sir Edward Elgar. Besides the two singers just mentioned we find Rosa Ponselle, Lauritz Melchoir , Elizabeth Schumann and Lotte Lehmann. Pianists include the composer Bela Bartok, Myra Hess, Walter Gieseking, and Artur Rubinstein . Wanda Landowska performed on the harpsichord.

Just as impressive in the 1931 book is a staggering list of BBC speakers for 1930. Drawn from seemingly every branch of intellectual endeavor we find such legendary authors as Virginia Woolf, T.S. Eliot, Andre Maurois, George Bernard Shaw and E.M. Forster. Among scientists, we encounter Albert Einstein, Oliver Lodge, James Jeans and Julian Huxley. Additionally, we recognize the economist John Maynard Keynes, anthropologist Bronislaw Malinowski, and Arnold Toynbee the historian. Einstein spoke on October 28, 1930, and his picture appears on page 34.

“BBC English” was for generations of Britons the standard pronunciation of their language. The accent did not arise by accident as a reader of the 1929 Handbook soon learns. An essay by A. Lloyd James observes that “The BBC is concerned only with questions of pronunciation, and the standard of pronunciation of its official speakers more and more, both within these islands and abroad, as a standard of accuracy to be aimed at.” He reveals that the BBC maintains an advisory committee on spoken English composed of such men of letters as The Poet Laureate of the UK, Robert Bridges, playwright George Bernard Shaw, and essayist Logan Pearsall Smith (an American!). It’s fitting that Shaw, the author of a play in which pronunciation is central, Pygmalion, should be on board.21 James, writing earlier in the 1928 Handbook, asserts, in an instance of naked snobbery, that “ [BBC English] seems to steer a course midway between the lapses of the uneducated and the affectations of the insufficiently educated.” For 3 pence one can buy a pamphlet from the BBC on how to acquire their pronunciation.22 Radio historian Mark Pegg observes that “…the accent of the announcers alone was to mark the social distinctions between the broadcasters and most listeners.”

Speaking of Shaw, perusing these BBC annuals one sees that radio drama was an important part of broadcast fare. The 1931 book remarks that 4 radio adaptations of plays of Shakespeare were performed the previous year. Shaw was represented with Captain Brassbound’s Conversion and St. Joan. Sometimes books and short stories were converted to radio plays, e.g. Joseph Conrad’s Typhoon and Lord Jim.

Andrew Crisell, a major British radio historian, convincingly defends the elitism of the BBC in the Reith years: “In pre-war Britain, universal education reached the age of about 14. Those temples of high art , the concert halls, opera houses and theatres were beyond the pockets of the great mass of people, and within the tiny minority who underwent higher education there was much more consensus than there is today about what in cultural terms was, good , significant or worthwhile.” Reith’s intention, he maintains, was to “… open up to all those who had been denied to them by a limited education, low social status and small income the great treasures of our culture.” 

TECHNICAL MATTERS

For those interested in the technical history of radio, the early years of the annuals are a treasure. These volumes contain a segment known variously as the Engineering or Technical Section. In addition there was sometimes a reference portion that was rich in technical information. Altogether, the technical content might occupy one third of the overall volume. By the late thirties these specialized sections were gone or much reduced.

The BBC did not patronize its audience. The level of discourse of the technical material is sometimes appropriate for degree holders in electrical engineering. Basically the information provided was of several kinds: technical advances and challenges facing the BBC engineering staff, help for the amateur home builder of receivers, which might include everything from schematic diagrams for radios as simple as crystal sets up to 6 tube superhetrodynes, construction of receiving aerials, wave propagation over a conducting earth, the role of the ionosphere in radio wave transmission, and a glossary of technical terms which contains for example: “Natural Frequency or Natural Period—The frequency or period at which a circuit containing inductance and capacity will naturally oscillate if set in electrical vibration. The natural frequency is given by the formula

cycles per second, where L is the inductance in henries and C is the capacity in farads. At this frequency, the condition of Resonance occurs.” [italics in original].

What is interesting about the schematic diagrams is that they never supply quite enough information for one to build a wireless receiver; the BBC did not encourage home construction. If someone bought a wireless set from a store there would be a record of her having purchased a radio. She might be less likely to avoid buying the half pound license fee than a home constructor of radios who left behind no trail. It’s possible that the Yearbook/Handbook did not encourage home construction out of fear of antagonizing their numerous advertisers of readymade radios. In the article “Some Hints for the Novice,” in the 1928 Handbook, the home builder is advised “In nine cases out of ten the results will be disappointing.” He (and it is always “he” in these articles) is then advised to buy the most expensive possible components if building a home set, and to eschew for example the “cheap foreign [valves]” because … “British valves are the best on the market.” Of course it was British valves that were advertised in these books.

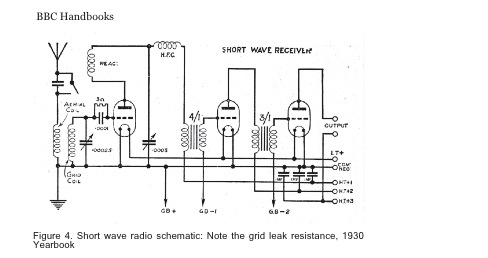
Sometimes one suspects that the information provided the hobbyist is not only deliberately sketchy but intentionally misleading as in this example (Figure 4) taken from page 341 of the 1930 Year Book. The schematic is for “… a simple but efficient shortwave circuit …and the values of the component parts should be near as possible to those given.” Not only are the values of some components not given but more striking is the value of the grid leak resistor connected to the fi rst valve on the left. Its value of 3: is off by a factor of one million.25 This might have been a careless error, but these books have so few typographical errors that one wonders if this wasn’t deliberate. 

In a situation where the BBC is seeking to enhance the listening experience, without encouraging the building of an entire set, they could be very helpful. The 1929 Handbook contains instructions for the construction of a wave trap 

to eliminate interfering stations. Page 343 contains a clear diagram (Figure 5) detailing construction of the inductor for the trap.

The use of a wave trap would increase the selectivity of a receiver. We are told in the same book that “the majority of ships” are using spark transmitters, a reminder that this crude technology, dating back to the early Marconi wireless telegraph era, was still in use. Wave traps were needed to block the resulting harmonics from reception.

The design of receiving antennas was of great interest to the set owner in the first decade of broadcasting, and the Handbooks/ Yearbooks recognize this with construction advice. We learn from the 1928 Handbook (p.249) that using an antenna whose overall length exceeds 100 feet violates the terms of your license, while the 1931 Yearbook advises the use of the entire allowed length. Moreover they tell you, “In general it is not a good policy to make an aerial system inconspicuous; for example it is bad practice to hide the horizontal portion of the aerial by running it close to the eaves or roof of the house. Although aerials of this type usually succeed in being inconspicuous they are seldom efficient, for their effective height is small. If the roof of the house is covered with lead, which is usually in electrical contact with the ground, the aerial in effect is only slightly higher than ground level.” The same book presents (p. 379) a possible arrangement for an aerial, given here in Figure 6.

 We notice how conspicuous this arrangement is; there is little chance that someone with this aerial would have the audacity to skip paying for a wireless license. One feels that this is not an accident. In fact there is no suggestion in any of the annuals that for someone using a regenerative or superhetrodyne radio, a much smaller indoor antenna might do. 27 As late as the 1940 Handbook (p. 98) the listener is advised to use an outdoor aerial.

The technical discussions in the Handbooks/Yearbooks of the early 1930’s could be at a very 

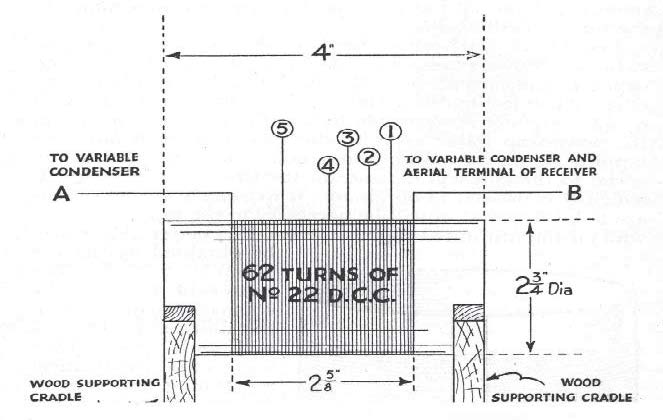
Figure 5. Inductor for a wave trap. 1929 Handbook

sophisticated level and this is most apparent in the chapter “Transmission” in the 1930 volume. Here we find an analysis of the direct and indirect waves in broadcast propagation that would be of most interest to radio engineers. A series of curves, based on Arnold Sommerfeld’s difficult mathematical theory of wave propagation over an imperfectly conducting spherical earth, shows the electric field strength vs. distance from the transmitter for various ground conductivities.

Of course engineers were also interested in the behavior of the indirect ray—the wave from the transmitter reflected back to earth by the ionosphere. The same chapter summarizes a paper delivered to the IEE by two members of the BBC staff, Peter Eckersley and a Mr. Howe, on this very subject. Using a mixture of theory and experimental results, the pair conclude that the strength of the signal returned to earth will be “.1 mv per meter for 1 kw radiated” at distances of from 300 to 1000 km. The preceding assumes a single reflection from what they call “the Heaviside layer.” Evidently credit was not to be given to Arthur Kennelly, who postulated such a layer independently and in the same year, 1902, as the Englishman Oliver Heaviside. Kennelly was an Irishman who was born in India and who settled in the United States, worked for Edison, and taught electrical engineering for decades at Harvard. It is not until the Yearbook for 1932 that we find the “Heaviside-Kennelly” layer and by 1934 the modern word ionosphere is used, perhaps reflecting the fact that it was by then known that there were several layers involved in the refraction of radio waves.

The British led the world, in 

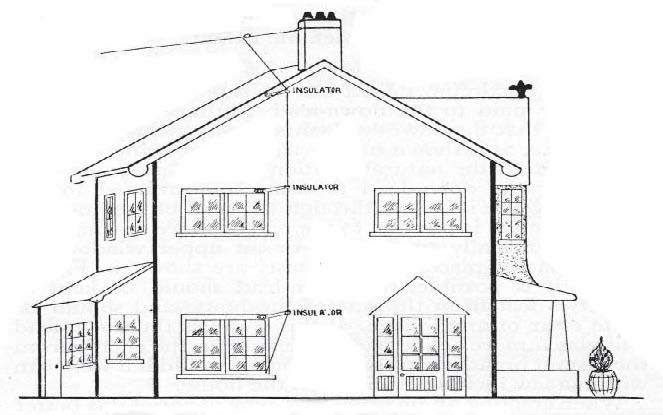
Figure 6. A suggested aerial. 1931 Yearbook

 providing regularly scheduled “high definition” broadcast television. From the 1937 Annual we learn that experimental t.v. was begun from Alexandra Place in London the previous year; one of its goals was to evaluate and compare the utility of two competing systems--the Baird and the Marconi-EMI. Both are discussed in some detail. The Baird would now be regarded in modern jargon as a “kluge;” it required a mechanical scanning disc, and worse, a photographic film as an intervening process in the transmission of the t.v. image. The book reports that in February of 1937 the Marconi-EMI system, which was all electronic, was adopted for permanent use, while the 1938 Handbook asserts that in 1937 the BBC was broadcasting 150 minutes of television per day with an estimated 10,000 people seeing the coronation of King George VI on their sets. By contrast, in the U.S. it wasn’t until 1939 that NBC began providing two hours of programs a week. The 1939 Handbook reports that, at the 1938 Radiolympia Exhibition in London, 22 firms exhibited televisions. 

If one were to read just one annual because of its technical content, it would be the 1930 Yearbook. Here we find four articles, written for the lay person, on science and engineering by acknowledged experts in their field. For example, Sir William Bragg, Nobel Laureate and Fellow of the Royal Society (FRS), addresses what physicists now refer to as the “wave-particle duality,” i.e. the fact that some physical phenomena can be explained only by treating the transmission of electromagnetic energy by means of a wave model, while others are explicable only by using a particle model. Bragg calls the particles “minute corpuscles proceeding from the luminous source.” In some respects the article is old fashioned—he avoids the modern term “photon” for the corpuscles in a stream of light. More curious is his use of the term “ether” to describe the medium in which both particles and waves propagate. The ether as a medium for electromagnetic radiation was discredited 25 years before with the publication of Einstein’s special theory of relativity and it is astonishing to find it still alive here.

Even more surprising is an article preceding Bragg’s titled simply The Ether and written by Arthur Eddington, FRS, one of the great British astrophysicists of the 20th century. His purpose is to proclaim his belief in the ether but he writes like a man on the defensive, acknowledging that we cannot ask what the ether weighs, is it a fluid or rigid, how fast does the earth move through it? He does concede that “A few distinguished physicists maintain that modern theories no longer require an ether—that the ether is abolished. I think that all they mean is that since we never have to do with space and ether separately, we can make one word serve for both together; the word they choose is ‘space.’” Since physicists speak of the properties of space ( e.g., the speed of light in space), Eddington would have us assign these properties to something called the ether—a throwback to the 19th century era of Maxwell’s modeling of the medium containing electromagnetic fields.

Although in Eddington’s day he might speak of a “ a few distinguished physicists,” no reputable physicist would, post World War Two, speak of the ether. Its demise was sealed by the eventual universal acceptance of Einstein’s work. What is especially puzzling about Eddington’s case is that he was the author of a very popular book explaining relativity: The Mathematical Theory of Relativity(1923). The Encyclopedia Britannica (15th edition) describes him as “the fi rst expositor of relativity in the English language.” Eddington has also written about his philosophy of science, which includes the concept of “unobservables” and the reader curious about his defense of the ether should read his work.

Of more practical interest tothe radio listener than the essays just mentioned is an article by Sir Edward Appleton, also an FRS. Appleton was to win the Nobel Prize in physics in 1947 for his research on the ionosphere and for his discovery in the 1920’s of what was for a time known as the Appleton Layer but which is now called the F layer of the upper atmosphere. He proposes to explain to the lay person the role of what he calls the Heaviside layer in radio wave propagation and why, as most listeners would have noticed, that certain stations are heard only at night and that the quality of their reception is highly variable. He also ties this variability to the sunspot cycle although what this connection is he does not explain— a reminder that the science of the upper atmosphere was still in its early years.

R. L. Smith-Rose was less well known than the three authors mentioned but his article, the fourth, on lightning and atmospherics is worth reading. Radio listeners were well aware of lightning, knowing it to be responsible for the clicks they might hear in their loudspeakers and headsets, especially in the summer. He explains the mechanism of lightning, the various kinds of lightning strikes, and the wavelengths of radio waves most apt to suffer from lightning generated noise. The article is accompanied by advice on how to “earth” [ground] your set to reduce the likelihood of lightning damage.

HISTORY BOOKS

The annuals for the period 1928 to 1940, with their summary of the previous year’s events in broadcasting, can be read as a history of Britain during a difficult, indeed terrible, period. As in the case of the technical content, what is sometimes most interesting is the excluded or partially presented material. The most salient example is to be found in the 1937 Annual. On December 11, 1936 King Edward the Eighth abdicated the British throne in order to marry his twice divorced love, the American, Wallis Simpson. The following day Edward broadcast a farewell using radio. His message was broadcast not only by the BBC domestic service but by BBC short wave to the entire world where in some countries, including the US, it was rebroadcast on medium wave. In the age of Empire, he had been monarch to over 500 million people. H.L. Mencken, the American critic, waggishly observed that this was “the greatest story since the Crucifixion.”30 The Annual has a one- line reference to the broadcast on page 47 while page 88 has an entry, inexplicably placed in a reduced font, about the farewell, and remarking that his valedictory “… was probably listened to by the largest broadcast audience on record.” The abdication was surely not Britain’s fi nest hour, but an event of this magnitude in the history of broadcasting cries out for more coverage. 

To read the Handbooks/Yearbooks in the period 1934 through 1940 can be a dismal business because one knows what is going to happen: Britain and much of the world is headed inexorably for World War Two. The 1934 Yearbook has a photograph of the newly elected Chancellor of Germany; Adolf Hitler assumed offi ce in January, 1933. We are told that with his election in Germany “the rebuilding of the bases of broadcasting has begun.” We learn that all employees of German radio who were Jewish or alleged to be “criminally suspect” were fired. The new head of German radio under the Nazis, Herr Hadamovksy is quoted: “My task… is to make broadcasting a sharp and reliable weapon for the government…” and furthermore “I have always ridiculed… the old idea that there is such a thing as objectivity and neutrality per se.” 

In the 1939 Handbook one of the larger sections is devoted to BBC coverage of “The Crisis [of 1938]”. It contains a photograph of a triumphant Neville Chamberlain at the Hester Aerodrome on September 30. He has just returned from Munich after meeting with Hitler. Mobile television units were at the airport, and the event was not only heard on the wireless but widely witnessed on British television. The Handbook proudly affirms that “ [television ] viewers were among the fi rst to see him holding aloft that fl uttering piece of paper (the writing was visible) bearing his own signature and that of Herr Hitler.” The Sudetenland of Czechoslovakia had just been handed over to Hitler in return for what Chamberlain would call “Peace in our time.”

Germany invaded Poland on September 1, 1939 and two days later Britain declared war on the aggressor. The 1940 Handbook, owing to wartime austerity, has shrunk to a mere 128 pages, less than a third of its size in its best days. The BBC knew that war was coming and followed advanced planning in which it was recognized that “peace time methods of transmission would endanger the national safety by giving guidance to enemy aircraft.”The Handbook explains that on the day of the invasion all stations shifted to a common programming material which became known as the Home Service and which initially used only two wavelengths, 449.1 meters and 391.1 meters. The long wave transmitter and various regional services were shut down as was all television; however short wave services to the rest of the world did continue and the long wave service resumed before the war’s end. Page 33 carries the text of Prime Minister Neville Chamberlain’s speech, which the BBC broadcast from 10 Downing Street on September 3, 1939. He states, “You can imagine what a bitter blow it is to me that all my long struggle to win peace has failed.” There is a touching photograph, opposite this page, captioned “Keep them happy, keep them safe” of children being evacuated from London.. 

One can in some respects trace the history of the war through the annuals. The 1941 Handbook has a photograph of the teenage Princess Elizabeth (the present day Monarch), accompanied by her sister Margaret, broadcasting a message to the children of the Empire. The same volume displays a picture of the results of a German air attack on the BBC headquarters at Broadcasting House in London. Again, this is one of those strange instances of partial reporting. On the 15th of October 1940 a 500 pound bomb landed in the BBC Music Library, killing 7 people, but the deaths are not mentioned.

Short wave and even medium wave services, especially to overrun countries, are discussed at length in the 1941 volume. We learn that “In Poland the Germans have made the possession of wireless sets illegal,” while in Czechoslovakia “anything broadcast by the BBC is known throughout the country in a few hours.” The same book has an essay by Harold Nicolson, Parliamentary Secretary to the newly formed Ministry of Information. He begins with a powerful summary of Hitler’s propaganda: “ His avowed method is to appeal to the lowest instincts in human nature, namely to envy , malice, greed, fear, and conceit.” Nicolson is at pains to explain that his new ministry will not be imitating the German propaganda chief, Jospeh Goebbels, but will indulge in “liberal propaganda,” which is based on “…true facts and common principles” and the belief “that there does exist a difference between right and wrong and that this difference is readily appreciated by the vast majority of mankind.” Facing the final page of the essay is a photograph of Winston Churchill, making his fi rst broadcast as Prime Minister, on 14 July 1940. The 1946 Year Book, the fi rst to appear after the war was over, remarks (p. 28) that, thanks to the BBC, Churchill’s words in the “darkest days” of the war were heard by 70% of the British population.

New in the 1940 Handbook is information about a wartime broadcasting service of the BBC which was to have consequences far beyond the hostilities. On the 19th of February 1940 broadcasting of the Programme for the Forces commenced. This went out on short wave as well as the medium wave 373.1 meters, later changed to 342.1 meters, and consisted of material designed for the men and women in uniform: news, popular music, dance music, swing, crooners, comedy. The content is described in the story “Listening with the Forces” by Major Richard Longland, BBC Liaison Officer with the Army. 

Many Britons on the home front listened to and enjoyed what became known as the General Forces Programme, a fact not lost on the BBC. In the 1946 Yearbook we find that the successor to the General Forces is the BBC Light Programme which went on the air in July 1945 essentially in competition in the UK with the still present traditional Home Service. There is a certain defensiveness in the description of the new service in the annual (pp. 53-54) : “The title Light Programme does not mean that everything broadcast on it must necessarily be frothy or frivolous,” although the unnamed author concedes that it does contain “a higher portion of sheer entertainment.” This same Yearbook has auguries of a new service in the annual for 1947: the birth of the BBC Third Programme.

The Third Programme was born on September 29, 1946, broadcasting from 6 p.m to midnight and was devoted to the high culture championed by Reith and his muse Arnold. There were no newscasts. An article by the novelist and travel writer Rose Macaulay on page 20 of the 1947 Year Book, “If I Were Head of the Third Programme,” gives some idea of what was broadcast, much of it serious music. She proclaims that the offerings were “proving more than all one hoped” with a week full of Beethoven’s String Quartets, and another of Byrd and Bach, and a performance of The Magic Flute. Modern music is not lacking – she speaks of Bax, Schoenberg and Webern. As for drama there were “good performances of the familiar great--Shakespeare, Ibsen, Strindberg, Shaw, Euripides.” The 1955 Handbook describes the Third Programme as intended for “Listeners of Cultivated Tastes and Interests.” 

Thus, a year after the war ended the BBC had become revolutionized in ways that Reith had never wanted nor perhaps envisioned. His Corporation was now a cake of three layers, with the Third Programme, Home Service, and Light Programme providing entertainment for high, middle and lowbrows. This was anathema to Reith who felt that the strength of the old, heterogeneous system was that the public was forced—if only by chance—to be exposed to some high culture. Indeed, Reith wrote in his diary that the new arrangement was “an absolute abandonment of everything I stood for.

Of course this restructuring and growing egalitarianism at the BBC was a manifestation of large social changes taking place in the UK. Even before the war ended the ruling Conservative party was voted out of control and Prime Minister Churchill was replaced by the Labour Party’s Clement Attlee on July 26, 1945. The frontispiece of the 1946 Yearbook is a photograph of the new Prime Minister. Railroads and coal mines were nationalized under the Labour Party and the National Health Service begun. 

The cover of the 1946 Yearbook (Figure 7) shows the dove of peace launched from a hand shrouded by bombed ruins.33 Alas, peace was short lived. In four years Britain and the United States would have troops in Korea. 

In the decades following the publication of this hopeful cover the Yearbook/Handbook would, like the BBC itself, became increasingly devoted to television. No book was published in 1953 or 1954 but the 1955 Handbook dwells on the banner broadcasting

 Figure 7. Launch of the peace dove. Cover 1946 Yearbook

 year of 1953—the coronation year of Queen Elizabeth II. In the UK alone, 12 million listened to the coronation on the radio but 20 million saw it on television (this out of a population of 41 million). This, reports the BBC, was the first time that the t.v. audience exceeded that of the wireless. Perhaps it is appropriate to end our examination of the books here. Finally, one wonders what would be the reaction of Sir John Reith if he could now see his BBC in the age of the Internet. The three layer cake that was BBC wireless in 1946 has today evolved into BBC services numbered one through seven. All go out as broadcast radio as well as Internet stations. Although some services are restricted to popular music and news, BBC radio 3, 4 and 7 have an abundance of serious music, lectures, and drama --Arnold’s “best that has been thought and said,” with some leavening from light entertainment. Of course, if you spend the day listening to one of the other services you’ll miss “the best”, and this would not please Reith.

SOURCES

 The entire run of Handbooks/ Yearbooks/Annual Reports is available on Microfilm from Microform Academic Publishers. http://www.microform.co.uk/archival-publishing.php This Microfilm edition is accompanied by a brief and useful discussion of their contents by British radio historian Hugh Chignell. The business branch of the New York Public Library has a complete set of the actual books. Lamont Library at Harvard University has them on microfilm as do doubtless many other university libraries.

ACKNOWLEDGEMENT

 I wish to thank Mr. David K. Nergaard and Ms. Naomi Ossar for useful assistance with this paper. The images presented here were in most cases reproduced by courtesy of the BBC. Mr. James Codd of the BBC assisted me with that procedure.

ENDNOTES

1 The Handbook was replaced by “The Handbook, Incorporating the Annual Report and Accounts” in 1974 and continued with that title until it ended in 1987. During the Great Depression, The Handbook diminished rapidly in size and was a mere 129 pages by 1938. In postwar years it grew but never achieved the heft of its early days.

2 The Yearbook was the title used in 1930-3, 1943- 1952. The title Annual was used in 1935-7. There is no consistency in spelling from year to year and one can find Year Book and Hand Book.

3 The artist is given simply as E. McK.Kauffer . This is E. McKnight Kauffer, a distinguished American illustrator from Montana, who was better known in Europe than at home. See the website http://www.aiga.org/content.cfm/medalistemcknightkauffer

4 Asa Briggs, The History of Broadcasting in the United Kingdom, vols 1-5, Oxford 1995 Andrew Crisell An Introductory H i s t o r y  o f  B r i t i s h Broadcasting, Routledge, 1997

5 Paddy Scannell and David Cardiff A Social History of British Broadcasting, volume 1, 1922-1939, Blackwell, 1991, p.5

6 An “experimenter’s license” was available for those choosing to construct their own sets.

7 An interesting comparison of British and American radio can be found in the essay British Quality, American Chaos: Historical Dualisms and What They Leave Out, Michele Hilmes, in Radio (vol2), Andrew Crisell editor, Routledge, 2009 pp. 62-85,

First-Hand:An Electrical Engineering Education at Cornell, 1956 - 1961

An Electrical Engineering Education at Cornell, 1956 - 1961

 

Submitted by A. David Wunsch, IEEE Life Senior Member, BEE Cornell 1961, PhD Harvard 1969

Historians of electrical engineering and education might be interested in what I experienced, more than 50 years ago, as an undergraduate student in a well regarded program at the Electrical Engineering School of Cornell University. I was there in the mid to late 1950’s as well as the early 1960’s. I suspect that these remarks might be of historical value because the nature of electrical engineering education has changed so profoundly in the years since I left Cornell. I can say this with some confidence as I became a professor of electrical engineering at another institution and taught there from 1969 until 2010.

I had about 160 classmates in my freshman electrical engineering class in the fall of 1956 and there were around 2000 first year students overall at the University. Of the 160 EE’s, exactly one was female, Carol D. I know that she felt self conscious—she once confided to me, “I feel as though I have three eyes.” She was gone by the end of our freshman year. I’m not surprised – neither students (I am guilty here) nor faculty made any attempt to make her feel comfortable. She was an attractive young woman who dressed well and was the object of a lot of unfounded ugly remarks, e.g., “She’s working her way through school one professor at a time.” I hardly need mention that the department faculty was all male—this woman had no mentor.

Not only did Carol disappear from the program but so would the majority of her 159 male classmates. We were in a 5 year program and by graduation day there were only about 60 of us left. Why this occurred is mostly the subject of the remainder of this memoir.

In 1956, five year programs in engineering were not uncommon—they have now vanished, to the detriment of the profession. It was believed at the time that a young engineer entering his or her life’s work needed ample exposure to the humanities and the social sciences to become an educated individual, someone not handicapped by the narrowness of a purely technical education. The logic of this was solid and Cornell’s policy -–long since abandoned—is one of the few positive things I can say about my experience there. As a 16 year old entering the university, I didn’t mind having an extra year of college to get a good taste of the liberal arts.

Incidentally, I was not the only 16 year old. In the entire freshman class of 2000 students I think there were 70 of us youngsters—mostly products of the New York City public schools, which would skip you a grade if they thought you could handle it. In general, most of my classmates in EE at Cornell were bright kids and had come from such prestigious high schools as Stuyvesant, Bronx Science and Choate. For many of these youths, getting flushed out of electrical engineering, and in some cases transferring to less demanding universities or entering the military, must have been an embittering experience.

I might also add that the entire cost of a year at Cornell in the 1950’s was $2000, which covered tuition, room, board and books. An additional year of study didn’t seem like an enormous financial burden while today it might mean an expense of $50,000 .

Looking at the courses I was required to take at Cornell to get my bachelor’s degree in electrical engineering, I can see that I was receiving an education suitable for circa 1925. This explains in large part the dreadful attrition rate in my class. None of the courses, by themselves, was overwhelmingly difficult. What made life hard, and at times overwhelming, was the sheer amount of work required of us. Not counting phys ed, we took typically 6 courses per semester (this was the era of compulsory ROTC classes at Cornell) and many of them I realize now had no place in a modern electrical engineering curriculum, one that was to be valid for the next 40 years of our professional lives. What we received was an old fashioned, between-the –wars electrical engineering education, embellished with a large dose of mechanical engineering. In our freshman year we EE’s were taking mechanical drawing, (5 hours a week for two terms), machine shop, casting and working of metals. On top of this was a core of important work that is still in engineering programs today: college English, calculus, chemistry, and physics. In 1956 most freshman college students had never seen calculus in high school, which made it hard going in college, rougher still if you had no time for serious study. Chemistry, physics, machine shop, casting of metals all had labs. Typically one had a free afternoon per week in which to think, relax, or, more usually, seek help in math or physics from our instructors, if we could find them.

Our class of 160 freshmen had exactly one faculty adviser in the Electrical Engineering Department, B. K. Northrop. He was an elderly, kind and good man, in poor health, and he died the next year, only to be replaced by another aged professor. The job of suitably advising a needy class this size was too much for any one professor, even a youthful one in good health. I, like most of my classmates, had been a “science whiz kid” back in high school and the sight of 50% on a Cornell physics test was a shock—nothing we had been prepared for—and we didn’t know what to do. Mostly we worked and worried.

If our freshman year was hard the next year was equally hellish. Again we were weighted with mechanical engineering topics—strength of materials, thermodynamics, statics and dynamics. These subjects were also covered in our physics courses but without the additional slide rule work and lab reports. We even had a dose of civil engineering with a required course in surveying—taking up an afternoon a week with our using transits on the arts quadrangle. I have no doubt that some classmate of mine, reading this, will tell me of how as a working EE he needed to know some surveying but such people are rare. Later, as upperclassmen, we had more ME material: fluid mechanics and machine design. The latter, much loathed, we called “machine disease.” What was insidious about these non-electrical courses was that they robbed our curriculum of subjects we should have been studying. In 1956 digital computers were not a brand new technology—they had proved their worth in the war. Yet, there was not one course required of us in computer programming, computer architecture, or logic circuits. No faculty adviser suggested that I take such a subject as an elective. Although post war electrical engineering was the age of electronics, we took 4 semesters of heavy electrical engineering, ( motors and generators) and just 3 of electronics. Of the latter, we had twice as much instruction on vacuum tubes than transistors although the transistor radio had been on the market since 1954 and it was obvious which way electronics was headed. I never learned a thing about information theory, radar or television. When I graduated after 5 years I still hadn’t learned the concept of a “bit” of information.

A Cornell EE undergraduate reading the above today would probably be incredulous. I know from recently speaking to one that there is an elaborate tutorial system in place to help people in trouble. “We won’t let you fail,” the old Heathkit motto that we undergraduates knew, is apparently now in place in Cornell engineering. An attrition rate such as the one I experienced would reverberate through the college rankings of US News and World Report. Moreover, if a class loses 90 students each paying 50,000 dollars a year to the university over a period of several years, the financial consequences, in the millions, are serious. While there may not be a huge number of female students, the 1 per 160 ratio that I knew is gone.

Everyone is my class was white, except for two Asians. We were a day’s drive from New York City but in 1956 Cornell apparently made no effort to recruit some black students there. I trust that there are some African-American students in Cornell EE now and the class is no longer as blandly homogenous as the one I knew.

The curriculum has been modernized—it’s no longer a mix of outdated power electricity and mechanical engineering. The EE School has a fine reputation and is very selective about whom it takes. I have to remind myself too that my experience was not unique to Cornell. Three of my high school classmates entered MIT in 1956—two in engineering and one in architecture. In a year, the two engineers were gone to liberal arts colleges. One friend went to Lehigh to take engineering and quickly left.

My bitter memories about Cornell remain but I do not wish to end on an entirely sour note. Thanks to the generous 5 year curriculum I was allowed to take some excellent electives: anthropology, 4 semesters of literature, advanced mathematics. I had some fine teachers for senior level elective courses in the EE department including William Gordon who designed the now famous Arecibo radio telescope in Puerto Rico. And I did learn to work hard.

Belmont, MA. July, 2012

“Mysterious Radio: Kipling and Cheever”

A. David Wunsch

“Any sufficiently advanced technology is indistinguishable from magic.”

 --- Arthur C. Clarke 1961

“The very fabric of life now she thought . . . is magic. In the eighteenth century, we knew how everything was done; . . . I listen to voices in America; I see men flying—but how it’s done I can’t even begin to wonder. So my belief in magic returns.”

 ---Virginia Woolf (from Orlando) 1928

A colleague—whom I will refer to as E.—asked one day that I step into his laboratory as he had something to show me. The audio tape that he placed inside a cassette deck had been used, he said, to record music and conversation, all of which he had carefully erased. He played this supposedly blank tape through his machine for me at high volume, during which in several instances he insisted that he heard a human voice—that of a dead relative. Buried somewhere in that painful white noise I did, at odd moments, hear something that might have been human, but nothing that I could discern as speech. Thanking him for his “interesting demonstration,” I left, having had my first experience with what I now know is a branch of the paranormal called “Electronic Voice Phenomena.”

Actually, I wanted to thank him for something else, but thought it prudent to keep my mouth shut. He had just treated me to a scene from the long history of the marriage between communication technologies and a belief in the supernatural. In E’s lab I felt transported back to western New York state to the company of the three Fox sisters who, in 1848—four years after Morse’s spectacular demonstration of his telegraph—asserted that they could decode the mysterious rapping heard inside their parents’ house—messages, they claimed, from the dead. These interpretations caused a sensation, and the three girls, who said that they had opened a “telegraph line” to another world, are credited with founding the modern Spiritualist Movement that spread through the United States and into the United Kingdom, and, as my friend had demonstrated, persists in various forms today. Central to this movement is the belief that the living can communicate with the dead.

The great advances in communication and transportation of the 19th century gave birth to the literature of science fiction—writing that we associate in that same century with two familiar names, Jules Verne and H.G. Wells—but which engaged the interests of

Rudyard Kipling (1865-1936)

other serious authors as various as Twain, Hawthorne, and Poe. Somewhat lesser known because of fame garnered in other genres, but equally interesting, are the fantasy and science fiction contributions of Rudyard Kipling. To students of radio and its ancestor the wireless telegraph, there is one short story of his that continues to fascinate: “Wireless,” which appeared in Scribner’s Magazine in August of 1902. This tale—in which the wireless telegraph apparently enabled a spiritualist experience—has attracted considerable scholarly attention.[1] Kipling is not the only highly regarded writer to exploit in fiction the apparent strangeness of electromagnetic communication, and we will look not only at his piece but also at a radio related story of John Cheever’s which appeared nearly 5 decades later. 

About Kipling’s decline in reputation as a writer, starting perhaps almost from the time of his Nobel Prize in 1907, I need say little here. Most people are astonished to learn that he died as recently as 1936—just 5 years before Woolf and Joyce—so identified is he with Victorian England. Some three dozen of Kipling’s stories continue, however, to be held in high regard by science fiction and fantasy buffs, and anthologies with generous introductions appeared in the late twentieth century.[2]

The scene of Wireless is an unnamed coastal British city. The time is presumably the present (1902), a fact evident from the contemporary technology. We are in a druggist’s shop, heavily illuminated by electricity, on a painfully cold winter Saturday night. The shop’s owner is absent, but his nephew, young Mr. Cashell, situated in a room connected to the store, is engaged in operating a wireless telegraphy set for sending and receiving Morse code. Tending the shop is an apothecary, Mr. Shaynor, who we will soon learn is dying of consumption.

There is an unnamed visitor, the narrator, a friend of the owner, who enters the shop to see the wireless set in action. Cashell explains to the narrator that he is trying to signal to the Marconi station in the city of Poole—he is waiting for Poole to “call us up”—and anticipates communication around midnight. While they are chatting, a young woman walks in and seeks to coax Shaynor into a “walk round by St. Agnes,” presumably a local church. Shaynor agrees, and the narrator mans the counter for him. Alone with Cashell, the visitor confesses to him that he is ignorant of exactly what electricity is. He receives the reply, “If you knew that you’d know something nobody knows.” Cashell then displays a device at the heart of his wireless receiver that will show the “magic” manifestations of Hertzian (radio) waves: the coherer, a glass tube with two tiny silver plugs and a quantity of metallic dust between them.

Shaynor returns without the girl. He is coughing blood, and the narrator, who has some knowledge of pharmacology, hands him a remedy he has formulated to give the poor man some comfort. While Shaynor dozes off from the medicine, Cashell gives his visitor a little lecture on wireless, explaining how a transmitted signal “ induces” a received signal. We also learn from Cashell that the name of Shaynor’s female friend is Fanny Brand.

Educated British readers in 1902 knew their romantic poets. Their mental antennae would have been raised by the girl’s name, the name of the church, the weather, Shaynor’s profession, and his terminal illness. All point to the poet John Keats (1795-1821) who died in his youth of consumption. He had studied both pharmacology and medicine. His mistress was Fanny Brawne, and, in 1820, he wrote the well loved poem The Eve of St. Agnes whose opening line is “St. Agnes’ Eve—Ah, bitter chill it was.” Shaynor’s girl resembles an image in an illuminated toilet water advertisement in the shop, so there is a double pun on the name Brand—she is both Brawne and a brand.

John Keats (1795-1821) Poet and Surgeon’s Apprentice

The narrator leaves Cashell in his lab-office and returns to the main shop to find Shaynor in a daze, fixated on the glowing simulacrum of his Fanny, and, in a tentative and imperfect way, reciting lines that are unmistakably from Keats’s The Eve of St. Agnes. Shaynor begins writing, and lines from the poem now emerge on paper. At this moment Cashell tries to draw the visitor into his office: “there’s something coming through from somewhere; but it isn’t Poole.” But the narrator is irritated at the interruption and tells him harshly: “Leave me alone till I tell you.” Shaynor continues with his writing and reciting, rendering the poem nearly correctly, and then moves to a bit of the same poet’s Ode To A Nightingale. Suddenly, he begins to shake and in a moment is out of his stupor, back to his normal self, and unaware of what has transpired. When questioned, he denies any knowledge of Keats and says, “Is he a popular writer?”

Cashell now moves the pair into his office to witness a “curious performance.” Two ships out of Portsmouth are trying to make wireless contact, but neither can detect the other’s message. Cashell tells his listeners that: “Their transmitters are all right, but the receivers are out of order, so they only get a dot and a dash there.” When queried about the cause, he explains: “God knows—and Science will know tomorrow.” Finally, the signal from Poole is heard, and Cashell asks the narrator if there is anything he’d like to tell them in reply. He declines: his interest in wireless has dimmed, and he wants only to get to bed.

In most interpretations of the story, the presence of the operating wireless set is the catalyst or medium that allows Shaynor to establish an invisible channel to Keats. It has been suggested that the inability of the two ships to communicate is due to wireless communication being diverted at that moment to convey or “induce” the poet’s words. Gillian Beer points out that the story raises the question of why we assume that only the medium of print allows us to commune with a dead author and asks us to consider the possibility that Kipling is suggesting that this novel medium of the Edwardian era might be similarly employed.[3]

It is easy to lose sight of how the communications technologies developed in the nineteenth century mystified and thrilled its witnesses. The Morse telegraph made possible nearly instant communication and for the first time reliably separated communication from

Sir Oliver Lodge (1851-1940)

Physicist and Member Society for Psychical Research 

transportation. Listening to an Edison cylinder one could hear the recorded voice of someone who had died, while the wireless telegraph made possible communication with no visible connection between sender and receiver. Kipling’s story takes advantage of this aura of mystery. Are we to imagine that Kipling himself believed that a scene such as the one he described was possible? I think not. His younger sister “Trix” suffered from mental illness for most of her life.[4] Modern Kipling biographers have diagnosed her as schizophrenic; she heard mysterious voices, attended séances, and indulged in “automatic writing” (like Shaynor) in a trance-like state.[5] All of this, together with her frequent hospitalizations, was disturbing to Kipling and it would be hard to imagine his assigning credibility to her delusions.

If Keats is the invisible major player in the story, there is yet another who isn’t named but who was alive when the piece was published, and who stands at the intersection of the major currents in the tale. The coherer, whose operation Cashell explains to his visitor, has a complicated history, but the term itself is attributed to Sir Oliver Lodge (1851-1940) who was to improve its sensitivity and who, circa 1894, was among the first to apply it to wireless telegraphy. Cashell’s coherer is much like the one Lodge employed. It is clear to wireless historians that, during the period of its use, no one really knew how the invention worked.[6]

Lodge was a distinguished physicist and educator. However, he had another life for which he was famous both in the UK and America, a life involving belief and research in psychic phenomena.[7] In 1884, he joined the Society for Psychical research, which was founded in 1882, with the purpose of investigating scientifically such questions as whether there is life after death and whether one might communicate with the dead. The Society exists today and is proud of past members who were distinguished scientists and men of letters including William James, who like Lodge was once President, Sir William Crookes, Sir Arthur Conan Doyle, Henri Bergson, and Alfred Wallace.[8] Although the organization has a record of unmasking fortune tellers, fake mediums, and other psychics, most of its members shared a belief in life after death and in the ability of the living to communicate with the dead. Kipling’s sister, using a pseudonym, participated in activities of the group.[9]

Lodge lost a son in World War I as did Doyle. Both soon reported having communicated with their dead boys. About a year after his son’s death, Lodge published a book about how he had exchanged messages with him by means of séances conducted with a medium. The book, Raymond or Life and Death, became a best seller principally as a result of the large number of British families that had suffered a similar tragedy.[10] Kipling’s son John died in the war, but his biographers don’t mention his resorting to a medium to reconnect with the youth. Indeed, some have suggested that his poem En-dor is an admonition against such practices as “the craziest road of all.”[11] 

The nature of invention in the nineteenth century and the first decade of the twentieth was virtually a guarantee that both inventors and their followers in the general public would be drawn to a belief in the supernatural. One easily overlooks how ignorant inventors of that period were of the basic science underlying their inventions. By 1880, the cities and towns of the United States had been linked for several decades by the electric telegraph, and there was a telegraph cable under the Atlantic Ocean that joined the United States and Great Britain. Electric illumination in U.S. cities via incandescent bulbs was only a few years off. Yet, Oliver Lodge could say in a public lecture in 1882: “What is electricity? We do not know. We cannot assert that it is a form of matter, neither can we deny it.”[12]

The modern theory of electricity—now only a little over a century old, and based on the electron as the elemental particle of charge—dates from J. J. Thomson’s experiments of 1897. It took several years for scientists to accept that these particles were essential components in our evolving understanding of the atom. Cashell’s ignorance of the precise nature of electricity would have been typical of wireless operators of his era.

In December of 1901—a year before the publication of Kipling’s story—Marconi and an assistant were in Newfoundland and reported repeatedly hearing the letter S in Morse Code sent by wireless telegraphy from a transmitter in England, the first wireless transatlantic message. The sensational news made the front page of the New York Times, but the achievement was dogged by a problem: It was known for several decades that electromagnetic waves, like visible light, traveled in straight lines once the wave was launched. The signals heard by Marconi obviously had managed to follow the curvature of the Earth, yet he could offer no explanation. In fact, the physical theory explaining the bending of waves when they reached the upper atmosphere, which permitted the success of the experiment, was not established successfully until 1924 and not by Marconi.

It was the work of Edward Appleton, who later was knighted and awarded the Nobel Prize in 1947. As early as 1902, Arthur Kennelly and Oliver Heaviside separately had conjectured the existence of a conducting layer in the upper atmosphere that reflected radio waves over the horizon.

These examples are not atypical. The triode vacuum tube, developed in 1906, was the crucial invention in radio for 42 years until the introduction of the transistor. Yet, Lee de Forest, the self-styled “father of radio” who discovered the triode, did not understand its principles.[13] A vast public came to believe that modes of communication in daily use required explanations that would be far in the future. It is no surprise to learn that in 1909, William James remarked that, in denying the possibility of spiritualism we might be “ignoring a natural kind of fact of which we do not yet know the full extent.”[14] Understandably, Cashell tells the narrator of the story that he cannot explain the failure in communication between the two ships, but that: “God knows— and Science will know tomorrow.”

In the era of the story Wireless, a core belief was that the electromagnetic waves in use for communication moved from transmitter to receiver through a medium referred to as the ether or aether. The ether was seen as a conduit for these waves just as air was required for the existence of sound waves. The medium of the ether was central to most nineteenth-century thought about electromagnetic waves but, unlike air which you could store in a balloon, the ether had never been detected. It is an example of the “natural kind of fact” that James spoke of, and it was at the center of Lodge’s spiritualistic beliefs. Where else did the dead and their voices reside but in the ether? As he put it, the ether is: “… where our existence lies, and there is our spiritual home.”[15]

The crumbling of a general belief in the existence of the ether dates from 1905 and the publication of Einstein’s theory of special relativity, which held that the laws of physics turn out to be exactly the same in all frames of reference moving at constant velocity with respect to one another. If the ether existed, an observer at rest in the ether would enjoy a privileged position in physics and directly contradict the new theory. Einstein’s work explained the negative outcomes of all experiments designed to detect the ether.[16] Gradually, belief in relativity took hold in the physics community, but not in the mind of Lodge who, at his death in 1940, clung firmly to a concept which by then had virtually no other proponents in the physics community.[17]

“Do you notice how their insane psychology attempts to infect the Universe? There is one Einstein, nominally a Swiss, certainly a Hebrew, who (the thing is so inevitable that it makes one laugh) comes forward scientifically to show that under certain conditions Space itself is warped and the instruments that measure it are warped also. . . . When you come to reflect on a race that made the world Hell, you see how just and right they should decide that space is warped, and should make their own souls the measure of Infinity . . . Einstein’s pronouncement is only another little contribution towards assisting the world toward flux and disintegration.”[18]

Although the wireless transmission of voice and music became possible in 1906, radio broadcasting in the United States began on a sustained basis only in 1920. Despite some resemblance of the hardware to that used in wireless Morse code transmission, we must regard radio broadcasting as a new medium, different from wireless telegraphy. Unlike the wireless telegraph whose termini were in offices, radio entered the home, and unlike its predecessors the phonograph and telephone, which also created disembodied voices, radio was a mass medium affording instant communication but which could be received in isolation. Jeffrey Sconce has documented how the new mass audience for radio created, at the same time, consumers of bizarre science fiction stories in which for example, a maniac broadcasts “a cursed piece of music that will draw its nation of listeners to mass suicide.” He remarks, with some hyperbole, that: “the institution of broadcasting came with a price: the invasion and dissolution of the private sphere of the home.”[19] 

In 1947, forty five years after the appearance of Wireless, John Cheever, who later won the Pulitzer Prize, published in the New Yorker one of his best known stories, The Enormous Radio.[20] In post-war America, a radio set was sufficiently commonplace so that one might imagine it to be as devoid of magic as the toaster. Nonetheless, the device still had sufficient aura of mystery so that a radio might plausibly become a catalyst for the supernatural in one fictional New York apartment. Some indication of the destructive magic— and in this story it is destructive—seemingly inherent in radio, can be seen in a letter written by Ezra Pound to a friend, just 7 years before the Cheever piece appeared, in which his new radio is referred to as a “Goddamn destructive devil of an invention,” “… a devil box,” and a “devouring serpent.”[21] We can look at the stories of Kipling and Cheever as a pair of markers embedded in the eras of wireless telegraphy and radio in which the authors exploit the strangeness attached to these inventions.

Cheever’s plot illustrates an invasion, to use the language of Sconce. The tale takes place in the apartment of Jim and Irene Westcott, who live in the comfortable Upper East Side of Manhattan. In their middle thirties, they have a seemingly agreeable life typical of their social class: they have two young children, a maid who also serves as a cook and nurse, and they frequently attend concerts and the theater. Their radio breaks down, and because of their interest in classical music, they buy an expensive replacement. The new set is ugly and gives off “a malevolent green light.” At first it works to their satisfaction, but Irene, who is home most of the day, soon discovers that the device picks up and rebroadcasts into their apartment music and voices generated within their very own apartment building.

They both initially enjoy the novelty of spying on their neighbors, learning their intimate secrets, and they spend an enjoyable evening so well entertained that they go to bed “weak with laughter.” But in the next two days, Irene continues what has become an addiction, and what she learns is distressing. A neighbor is having an affair with the building’s handyman, another woman is a “common whore,” a man beats his wife, a neighbor sells a diamond that a guest has accidentally lost at a recent party. A sick woman cannot afford more visits to the doctor. Irene is tormented by her new knowledge. Her appearance changes from one of cheerful innocence to “radiant melancholy.”

Jim arranges for a repairman to fix the set, but their lives are not mended. He begins to fret about their financial situation, and he reproaches Irene for her extravagance. Irene is terrified lest his voice be broadcast to the neighbors through their own radio. Jim explodes at her apprehension and reminds her of some ugly truths with which they have, until now, apparently lived without rancor: Irene has had an abortion or as Jim puts it, “went off to have that child murdered.” Irene has cheated her sister on their inheritance. She moves to the radio, hopeful that she might hear the neighbor’s nurse saying something soothing to the children she cares for, but the repaired set flatly reports news from the outside world, including a railroad disaster that has killed 29 people and some information on temperature and humidity. The Westcotts will not be the same.[22]

If Keats’s St. Agnes resides openly in the Kipling story, the Book of Genesis slithers beneath this one. The ugly radio set with its green glow evokes the snake in the tale of Adam and Eve. There is even a passing reference to an apple core. Pound’s comparison of radio to a “devouring serpent” is apt here. It would be simplistic to read this story as a critique of technology. It is, more broadly, a statement of the torment that awaits us when we become aware of the meanness, dishonesty, and cruelty in the world. We might then see these very aspects of our own lives. The tale condemns the cliché that one’s pain becomes more bearable, if one places it in the context of the sufferings of humanity.

The mechanism whereby an ordinary home radio becomes an eavesdropping device is technically preposterous, and there is nothing in Cheever’s biography to suggest he imagined it plausible.[23] It is plausible, though, that Jim and Irene, ignorant like much of the public of the physics of radio, would be prepared to accept the tale’s premise. We also should keep in mind that, during the 1940s, AM radio receivers often did pick up strange and inexplicable sounds (especially in city apartments). This observation is doubly true for the period of wireless telegraphy appearing in Kipling. The FM radio that most of us listen to provides little in the way of mysterious noises that were once commonplace.

In the very year that The Enormous Radio appeared, the transistor was introduced to the world by three U.S. physicists at Bell Telephone Laboratories. These men, all with PhDs in physics, understood the quantum mechanics that explained their invention which was to revolutionize the construction of radios—and all electronics—over the next decades. Unlike the coherer, the vacuum triode, and radio propagation over the horizon, there was no whiff of mystery to this device that replaced the radio tube. The absence of this aura is characteristic of most of twentieth-century inventions with which we are familiar, and it perhaps explains why mainline (i.e. non-science fiction) writers are no longer producing stories such as Wireless and The Enormous Radio.

To be sure, there are still small societies of believers using radios or recording machines to communicate with the dead. A collection of essays, Radiotext(e), contains Radio From Beyond the Grave by Carola Morales, who describes her group: The American Association for Broadcast Voice Phenomena.[24] They are “one hundred strong” and report hearing George Washington and Adolf Hitler. The reader can find the organization’s site on the Web in addition to one for the American Association of Electronic Voice Phenomena, to which my friend E with the “erased” tape belongs.

To an electrical engineer, there is something miraculous about radio—but not the miracles reported by such groups. The wonder is in the engineering itself. The electrons on the rabbit ears antenna that I’m using at this moment to hear a college FM radio station are moving about in a highly complex pattern, altering their behavior millions of times per second. Yet my radio, tuned to 95.3 MHz, has made itself sensitive only to that motion—vibrations of the current taking place in a small spectrum centered at 95.3 million times per second. The current itself is tiny—it’s measured in millionths of amperes. The radio senses that minute current and turns it into Beethoven. Now that is a miracle.

If the plot of John Cheever’s The Enormous Radio rings a bell, you may be recalling its adaptation for television. The story originally ran in the May 17, 1947, issue of The New Yorker. Forty years later, on May 17, 1987, the episode “The Enormous Radio” aired during the third season of the Twilight-Zone-esque series called Tales from the Darkside. The teleplay was by Guy Gallo; the director was Bill Travis. A trivia note: The enormous radio is a Majestic Multisonic manufactured in West Germany by Grundig. The first televised version of Cheever’s short story, however, was on the first season of The Revlon Movie Theater and aired on July 21, 1953. The teleplay was by Reginald Rose; the director was Daniel Petrie. That production featured Darren McGavin, who performed in many of the classic anthology dramas of the 1950s and starred as Mike Hammer (1958- 1959). Source: Internet Movie Database www.imdb.com

David Wunsch

Department of Electrical and Computer Engineering

University of Massachusetts Lowell

Lowell, MA 01854

David_Wunsch@uml.edu

Bio note: A. David Wunsch is Professor Emeritus of Electrical Engineering at the University of

Massachusetts Lowell where he teaches a course on the principles and history of radio.